Multiplicación(Continuación).
Ejercicio 2
Calcula los productos posibles entre las siguientes matrices: Lo que nos piden en este ejercicio es multiplicar las matrices que se puedan multiplicar. Para ello, el número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz.
Lo que nos piden en este ejercicio es multiplicar las matrices que se puedan multiplicar. Para ello, el número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz.
Vamos a empezar con la matriz A que tiene 3 columnas. Esta matriz la podremos multiplicar por las matrices que tengan 3 filas. En primer lugar, la podemos multiplicar por la misma matriz A, que también tiene 3 filas.
Realizamos el producto de matrices de A.A= Multiplicamos filas por columnas:
Multiplicamos filas por columnas: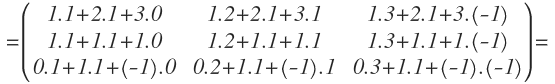 Y operamos:
Y operamos: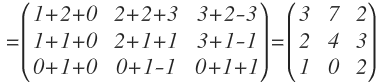 La matriz B también tiene 3 filas, por lo que podemos realizar la multiplicación de A.B=
La matriz B también tiene 3 filas, por lo que podemos realizar la multiplicación de A.B= Multiplicamos filas por columnas y operamos:
Multiplicamos filas por columnas y operamos: Seguimos con la matriz B que tiene 1 columna. La podemos multiplicar por cualquier matriz que tenga 1 fila, pero en este caso no tenemos ninguna, ya que la matriz A tiene 3 filas, la propia matriz B tiene 3 filas y la matriz C tiene 2 filas. Por tanto, la matriz B no la podemos multiplicar por ninguna matriz.
Seguimos con la matriz B que tiene 1 columna. La podemos multiplicar por cualquier matriz que tenga 1 fila, pero en este caso no tenemos ninguna, ya que la matriz A tiene 3 filas, la propia matriz B tiene 3 filas y la matriz C tiene 2 filas. Por tanto, la matriz B no la podemos multiplicar por ninguna matriz.
Por último vamos a ver los posibles productos de matrices con la matiz C. La matriz C tiene 3 columnas, por lo que la podemos multiplicar por matrices que tengan 3 filas.
La matriz A tiene 3 filas, por lo multiplicamos C.A: Multiplicamos filas por columnas:
Multiplicamos filas por columnas: Y operamos:
Y operamos: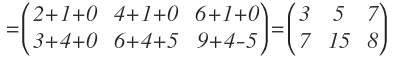 La matriz C también se puede multiplicar por la matriz B, que tiene 3 filas:
La matriz C también se puede multiplicar por la matriz B, que tiene 3 filas: Multiplicamos filas por columnas y operamos:
Multiplicamos filas por columnas y operamos: Ahora que ya sabes cómo multiplicar matrices, vamos a ver las propiedades del producto de matrices cuadradas.
Ahora que ya sabes cómo multiplicar matrices, vamos a ver las propiedades del producto de matrices cuadradas.
Calcula los productos posibles entre las siguientes matrices:
 Lo que nos piden en este ejercicio es multiplicar las matrices que se puedan multiplicar. Para ello, el número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz.
Lo que nos piden en este ejercicio es multiplicar las matrices que se puedan multiplicar. Para ello, el número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz.Vamos a empezar con la matriz A que tiene 3 columnas. Esta matriz la podremos multiplicar por las matrices que tengan 3 filas. En primer lugar, la podemos multiplicar por la misma matriz A, que también tiene 3 filas.
Realizamos el producto de matrices de A.A=
 Multiplicamos filas por columnas:
Multiplicamos filas por columnas: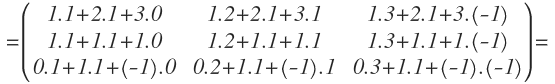 Y operamos:
Y operamos: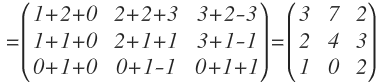 La matriz B también tiene 3 filas, por lo que podemos realizar la multiplicación de A.B=
La matriz B también tiene 3 filas, por lo que podemos realizar la multiplicación de A.B= Multiplicamos filas por columnas y operamos:
Multiplicamos filas por columnas y operamos: Seguimos con la matriz B que tiene 1 columna. La podemos multiplicar por cualquier matriz que tenga 1 fila, pero en este caso no tenemos ninguna, ya que la matriz A tiene 3 filas, la propia matriz B tiene 3 filas y la matriz C tiene 2 filas. Por tanto, la matriz B no la podemos multiplicar por ninguna matriz.
Seguimos con la matriz B que tiene 1 columna. La podemos multiplicar por cualquier matriz que tenga 1 fila, pero en este caso no tenemos ninguna, ya que la matriz A tiene 3 filas, la propia matriz B tiene 3 filas y la matriz C tiene 2 filas. Por tanto, la matriz B no la podemos multiplicar por ninguna matriz.Por último vamos a ver los posibles productos de matrices con la matiz C. La matriz C tiene 3 columnas, por lo que la podemos multiplicar por matrices que tengan 3 filas.
La matriz A tiene 3 filas, por lo multiplicamos C.A:
 Multiplicamos filas por columnas:
Multiplicamos filas por columnas: Y operamos:
Y operamos: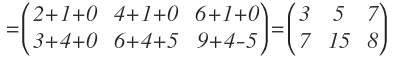 La matriz C también se puede multiplicar por la matriz B, que tiene 3 filas:
La matriz C también se puede multiplicar por la matriz B, que tiene 3 filas: Multiplicamos filas por columnas y operamos:
Multiplicamos filas por columnas y operamos: Ahora que ya sabes cómo multiplicar matrices, vamos a ver las propiedades del producto de matrices cuadradas.
Ahora que ya sabes cómo multiplicar matrices, vamos a ver las propiedades del producto de matrices cuadradas.
Comentarios
Publicar un comentario